A goal of mine is to give everyday people tangible reasons to trust their hardware. Betrusted is a multi-year project of mine to deliver a full-stack verifiable “from logic gates to Rust crates” supply chain for security-critical applications such as password managers. At this point, many parts of the project have come together: Precursor is an FPGA-based open hardware implementation, and it runs Xous, our Rust-based microkernel message-passing OS. I currently use my Precursor on a daily basis with the “vault” application loaded to manage my passwords, TOTP tokens, and FIDO/U2F logins.
However, Precursor is expensive, because FPGAs are expensive. The device could be much cheaper with a dedicated security chip, but then we have no reason to trust these chips – security chip vendors don’t facilitate any form of user-side inspection, so we can’t tell if we have real or fake security chips in our device.
Kind of defeats the purpose, if you ask me.
Last March, I introduced the concept of Infra-Red, in situ (IRIS) inspection of silicon in a blog post and an arXiv paper. My hope has been that IRIS, plus some circuit-level scans and mathematical methods, could be the missing link that allows us to transition from our expensive FPGA-based Precursor solution, to a more pocketbook-friendly ASIC-based solution.
At the time when I released the initial paper, every picture was manually composed and focused; every sharp image was cherry-picked from dozens of fuzzy images. It was difficult to reproduce images, and unsuitable for automatically tiling multiple images together. The technique was good enough for a demo, but shaky as a foundation for full-chip verification.
Over the past year, I’ve refined the technique and implemented a fully automated system that can robustly and repeatably image whole chips at micron-scale resolution in a matter of minutes. The idea is not for everyone to have one of these robots in their home (but how cool would that be!); rather, the idea is that most users could utilize an inexpensive but somewhat fiddly setup and compare their results against reference images generated by the few users like me who have fully automated systems.
Here’s an example of the MPW7 run on SKY130A, courtesy of Matt Venn, imaged using my automated IRIS machine:

The above is just a thumbnail; click on the image to zoom into and browse the full-resolution version at siliconpr0n.org (and check out my collection on that server for some more full-chip IRIS images). Each of the mottled dots in the lighter-shaded rectangles in the image corresponds to a logic gate, flip flop, or a “fill cell” (dummy transistors wired up as decoupling capacitors). To create the image, I just had to tell the machine where three corners of the chip are, and it automatically focuses and scans the full area. A script then post-processes the tiles into the fully-composed image you see here.
A broad goal of the project is to democratize silicon imaging and improve the state of the art in hardware verification. This is an area where simply popularizing silicon imaging can move the needle on security for everyone, because a credible threat of being caught reduces the incentive for adversaries to invest in expensive Trojan-implantation capabilities.
The good news is that the project is now at a state where, over the next couple of months, I can share a series of posts that detail the methodology used to develop the automated IRIS system, as well as document the construction of the device.
To kick things off, I’m going to start with a review of the current state of the art in hardware verification.
Review: Current State of the Art in Hardware Verification
Is my computer trustworthy? How do I know it was built correctly, and will execute my instructions faithfully? These are the questions that hardware verification aims to answer.
Hardware verification happens at every level of the supply chain. Let’s start with the relatable, every-day problem of how do I pick a piece of hardware to buy, and from there dive all the way down to esoteric topics such as verifying the circuits and devices that make up the hardware itself.
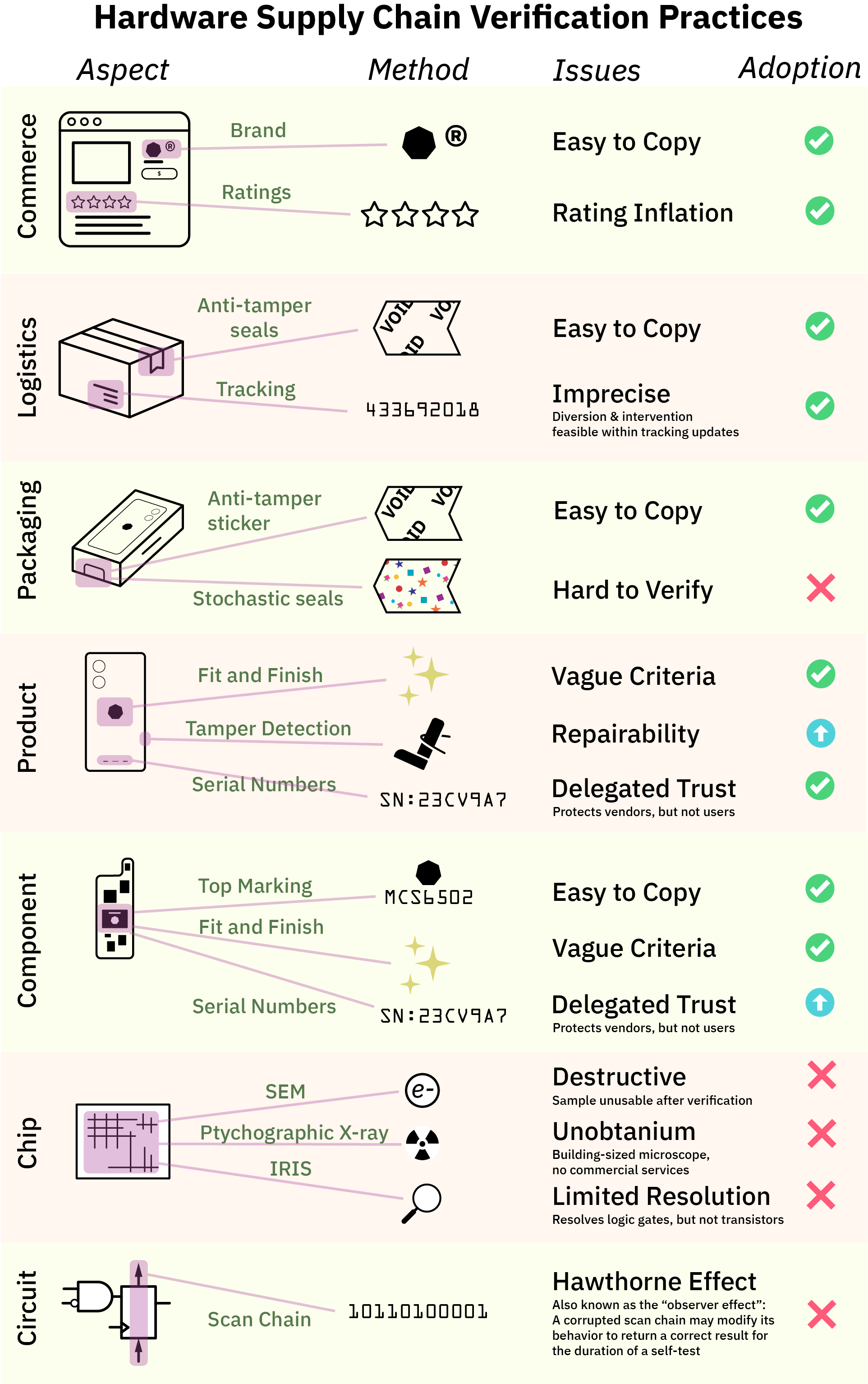
Consumers shopping for a computer rely principally on reputation mechanics to make choices: is the manufacturer a reputable brand? And how do my peers rate it?
Many of us can relate to how these mechanisms can fail. Ratings can be inflated by purchasing fake reviews, and stores can sell counterfeit brand goods. “Surely, this is just a problem of the retail market”, one might think. Once we’ve waded through the swamp of advertisements and on-line storefronts, the powers that be ought to ensure the device we ordered is the device we get! Otherwise it’s like, fraud or something bad like that, right?
Unfortunately, the level of sophistication for verification at every level of the supply chain is precisely as much as it needs to be for the vendor to get away with it, and not one iota more. For example, when it comes to logistics, we largely rely upon anti-tamper seals and tracking numbers to make sure our package arrives intact.
These measures are generally effective at deterring petty theft, but most anti-tamper tape can be purchased by the roll on gray markets, and tracking updates are too infrequent to rule out package diversion and intervention. Besides, that, consumers are conditioned to accept packages that have been mis-routed or experienced an “exception” during delivery – few will return an item that was delivered a day late under fears that the item could have spent a night in a facility where back doors were installed. Our ready acceptance of delivery exceptions is just one example of how supply chains are only as tight as they need to be for broad consumer acceptance, and not one iota more.
Once you’ve received the shipping box, most high-end consumer electronics have additional seals on their packaging. Unfortunately, most seals rely on easy-to-copy anti-tamper solutions such as holograms or fine printing; or at best contain serial numbers that are easy to copy yet have no easy way to check for authenticity.
Solutions such as glitter seals or other stochastic seals that rely upon the randomness inherent in paper fiber or glue to create a unique, unforgeable seal for every package have been proposed, but adoption is low and there is a lack of standardized, easy-to-use verification tools for such seals. Again, packaging seals are just as good as they need to be for broad consumer acceptance, no more, no less.
At the product level, there is a modicum of good news, at least in certain classes of products.
The traditional route of verification – observing the “fit and finish” of a product to detect counterfeits – is still the dominant method for most consumer products. However, in mobile phones and some laptops, manufacturers deploy electronic serial numbers and tamper detection techniques to deter would-be thieves of components or sub-assemblies. The effectiveness of these techniques depend intimately upon the implementation details; but in any case, they incur a cost in repairability and often times the end consumer can’t access the vendor’s databases to check that everything is in order. Instead, consumers are forced to delegate their trust to the vendors; yet regular consumers have no way to audit the vendors. The deferred trust boogeyman haunts everything from Apple’s iPhone ecosystem, to Intel’s SGX remote attestation mechanisms.
One would hope that this increase in verification sophistication is a trend that improves the deeper you go into the underlying technology. Unfortunately, it’s quite the opposite.

At the component level, the standard to this day for verifying the authenticity of a component is to look at the top marking (that is, the laser-etched numbers and logo) and the fit and finish of the package. Counterfeiters will often miss subtle details such as the font of the numbering, the location of the pin 1 marking, the composition of the overmold material, etc. Factories train staff to inspect and detect defects based on these irregularities.
What happens when a counterfeiter gets all these factors right? Well … the component goes into production, and we find out later about problems, either due to the assemblies failing test in the factory, or perhaps failing in peculiar ways in the field. For better or for worse, these problems are rare, generally affecting less than single-digit percentages of end users, and absent specific requirements or payments from customers to do more, equipment makers do exactly this and nothing more to protect the supply chain.
Even though most modern microcontrollers ship with an electronic serial number, few device manufacturers take advantage of them, and, perhaps somewhat surprisingly, there is usually no easy way to authenticate serial numbers with the component maker. Often times the purpose of the serial number is to serve as a unique ID for tracking products once manufactured; they are not structured to serve as a cryptographic method for determining provenance of the chip itself. Some security-forward microcontrollers feature things like PUFs (physically unclonable functions), but their implementation is usually directed at preventing people from tampering with or servicing their devices, rather than enabling users to verify the construction of the device itself.
And that’s about it – this is where any attempt to verify our electronics stops. To a first order, nobody even looks at the wires inside the chip.
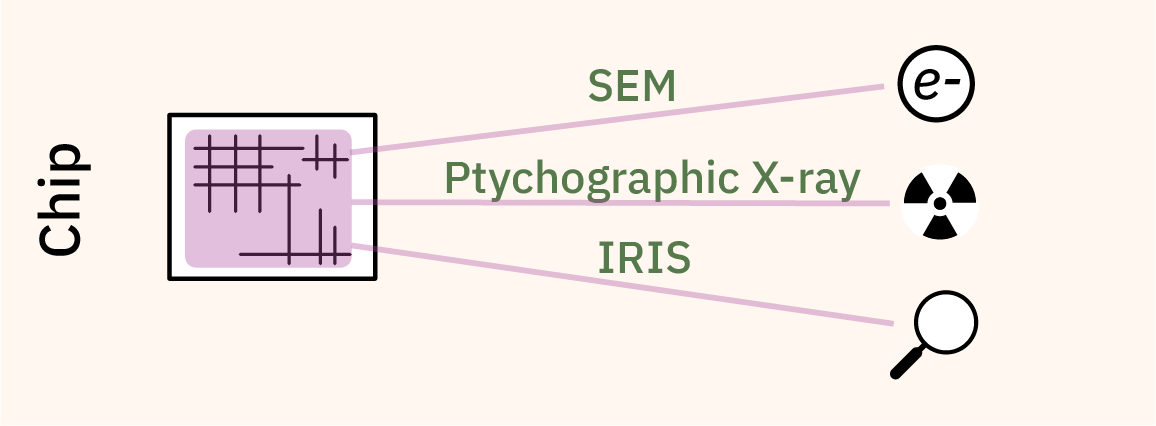
This is because prior to IRIS, your options for inspecting silicon are either destructive, or experiments conducted in high energy physics labs. If you’ve ever seen the brilliant teardowns done by companies like TechInsights, the chips are generally imaged at the circuit level with a SEM or FIB, which requires the chip to be removed from its package and some of the metal layers to be permanently stripped off. Thus, one can obtain extremely high-quality imagery of a sample chip, but these techniques cannot be used to verify the very chip you want to use inside your computer, as the imaged chip must be destroyed.
An alternative, non-destructive technique known as X-ray ptychography can be thought of as a very high resolution 3D scanner for circuits. It’s very impressive, but to date it can only be done in a handful of high energy physics labs and it takes a long time (about three hours for 20 cubic microns) to image a full chip.
The technique I’m developing, IRIS, is a non-destructive technique to acquire micron-resolution images of the first metal layer of a chip at a rate of a seconds per square millimeter. To the best of my knowledge, this is the first practical technique that gives users a glimpse of the actual circuits they will use after it has been mounted on a circuit board.
There’s one final layer deeper into the technology stack beyond imaging of the circuits: electrically testing the circuits directly with a technique known as a “scan chain”. The good news is that scan chains are a mature technology; the bad news is that it is almost never done by users because the details of the scan chain are kept secret, and that a scan chain inspection alone can be easily defeated by a malicious adversary.

The purpose of a scan chain is to assist with the rapid detection of fabrication defects. It works by adding an extra path to a finished design that strings every register into one or more chains. Bit patterns are loaded into the chain, and the resulting logical operations performed by the gates connected between the registers is observed on the output of the chain. With enough patterns, you can build up an idea of what logic is between every register. Of course, the space of bits to explore grows exponentially with the number of bits in a chain, so it’s not practical to brute-force a large state space.
As a result, scan chains are good for detecting flaws in known circuits introduced by mother nature, but ineffective at deterring a malicious adversary. This is true even if one could brute-force the entire state-space due to the epistemic circularity of trusting a circuit to test itself. More colloquially, one may have heard of the “Hawthorne Effect” or the “observer effect”, which describes a subject under study temporarily altering their behavior because they know they are being studied, thus affecting the results of the study. In this case, a scan chain knows when it’s being queried, and thus, a malicious modification to a scan chain can add hidden states that alter its behavior for the duration of a scan, allowing it to pretend to be correctly constructed, but only when a check is actively running.
Although almost every chip goes through a scan chain test before it is shipped, the test vectors are proprietary, and often times the scan chains are deliberately and permanently sealed in a way to make it impossible for users to access. Scan chains may be scuttled after the factory test for ostensible security reasons, as an adversary can use them to read out the full state of a chip. However, depending on the threat model, it may be preferable to give users the option to exercise the scan chain and then permanently fuse out the scan chain after inspection.
Filling in the Verification Gap
As the summary chart below shows, supply chain verification techniques, although imperfect, enjoy broad adoption at the component level and above. However, there is a significant gap in user verification starting at the chip level and below.
My work, the Infra-Red, in situ (IRIS) inspection of silicon, is a step toward filling in this verification gap. In its simplest form, chips are deliberately constructed for optical inspection with infra-red light shined through the back side of the chip – that is, the side facing “up” that is not bonded to the circuit board.
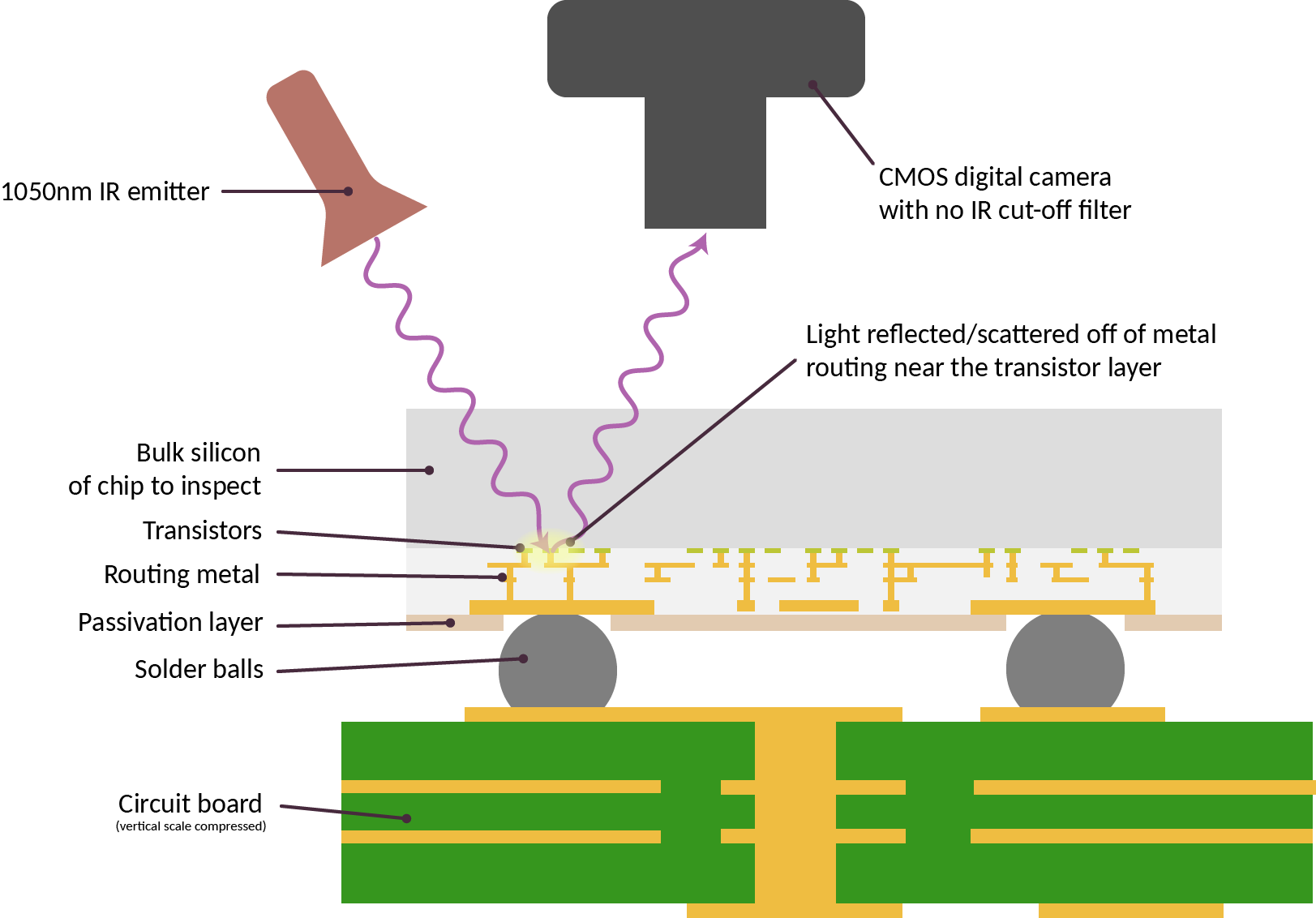
The technique works because although silicon looks opaque at visible light, it is transparent starting at near-infrared wavelengths (roughly 1000 nm and longer). Today’s commodity optics and CMOS cameras are actually capable of working with lights at this wavelength; thus, IRIS is a low-cost and effective technique for confirming the construction of chips down to block level. For example, IRIS can readily help determine if a chip has the correct amount of RAM, number of CPU cores, peripherals, bond pads, etc. This level of verification would be sufficient to deter most counterfeits or substitutions.
However, due to the diffraction limit of infra-red light, it is insufficient for transistor-level imaging. Furthermore, it can only reliably infer the existence of the metal layers closest to the transistors (in technical jargon, it can infer the existence of “standard cell” library elements); it cannot reveal too much information about the higher-level metal wires that route between logic gates.
Thus, for threat models which require protection against adversaries capable of manipulating wires on an integrated circuit, IRIS should be combined with scan chain techniques to robustly verify a chip’s construction.
Hybrid Verification For the Win
As alluded to previously, scan chains alone are insufficient for detecting modifications to a circuit, because an adversary may modify the scan chain in such a manner that it responds with correct answers during the scan itself, but behaves maliciously otherwise.
However, such modifications require the introduction of additional logic gates to track the scan state and compute both correct and malicious responses. Because IRIS can “see” logic gates, it is able to put a firm upper bound on the potential amount of additional logic present in an integrated circuit. Thus, the combination of IRIS and scan chain techniques may be able to effectively verify that a circuit is correctly constructed.
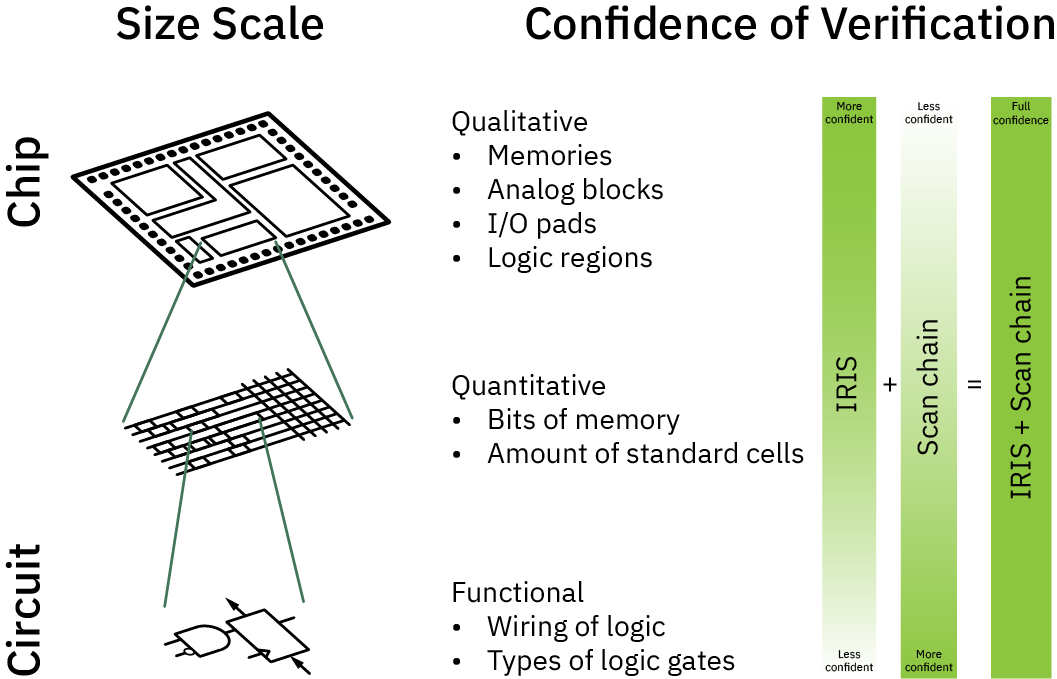
The diagram above illustrates how IRIS and scan chain techniques compliment each other to obtain a high-confidence verification of a chip’s structure.
- At the largest scales, IRIS can trivially quantify the number of IP blocks, pads, analog functions and memories; this is in contrast to scan-chain techniques which may struggle to characterize analog functions and other macro-scale properties, due to factors such as the analog limitations of scan chains, and the exponential growth of state-space to explore at the macro-level.
- At intermediate scales, IRIS can quantify the number of bits of memory, or bound the number of standard cells in a region. This places constraints on how much malicious logic could be injected that could otherwise defeat a scan chain test.
- At the smallest scales, IRIS cannot discern individual wires or gates. However, scan chain excels at exploring the topology and function of logic at the smallest and most local increments.
Thus, in combination, the two techniques may be used to achieve a high confidence verification of a chip’s function – at a cost and time scale suitable for point-of-use (e.g. end user) verification. I say “high confidence” because in the end, there is a probabilistic nature to both imaging and scan chain pattern coverage. As future work I’d like to explore the possibility of using formal methods to mathematically rule out any escapes, but absent formal proofs, it is important to understand that the technique is probabilistic in nature. That being said, it is still vastly better than the current state of the art, which is doing nothing at all.
Hybrid verification could be a viable path toward filling in the verification gap at the most fundamental levels of the supply chain, assuming chip vendors are willing to facilitate such verification by designing and packaging their products in a manner conducive to optical verification, and assuming chip vendors are willing to share scan chain test vectors with end users.
IRIS: Where We Are, and Where We are Headed
Because of the 1000 nm wavelength limit imposed by the transparency of silicon, IRIS has a limit on the features it can resolve. Below is an example IRIS imaging a small part of a RISC-V core on a 130nm chip fabricated using the SKY130A open PDK from Matt Venn’s MPW7 run; you can browse the entire chip image here.
Use the slider to compare the base image against an overlay derived from the design files. Each colored rectangle in the overlay corresponds to a “standard cell”: blue are flip flops, pink are filler/capacitor cells, aqua are varieties of and-or-invert gates, etc. Note that the native resolution of the image above is 1469 pixels wide; it has been scaled down to fit the width of this page.
One can see that in a 130nm process, IRIS has a reasonable chance of conducting a gate-count census of an entire chip. And yes, it’s not atypical for chips to be limited not by logic density, but by wiring density; hence, the majority of a chip’s active area contains filler cells (the pink rectangles).
Above is of an identically scaled region of a 22nm chip, again of a RISC-V core, but this time almost the entire core is within view because the logic gates are, unsurprisingly, much smaller: a single gate can be as small as a few pixels. At this node, IRIS can place an upper bound on gate count to within a couple dozen extra flip flops.
An important caveat when comparing images above: the backside finish of the 130nm chip is a mirror polish, but the 22nm chip only went through backgrinding; in other words, the 22nm chip’s image clarity is degraded due to a series of small surface ridges that refract light. If the 22nm chip had the same mirror-finish quality as the 130nm chip, the imaging resolution of the 22nm chip would be improved. Back side polishing of chips is not a difficult or uncommon process, but it’s not done unless explicitly required. Thus, chips intended for optical verification should specify a high quality mirror finish for the back side.
IRIS goes hand-in-hand with electrical scan chains to achieve full chip verification. Scan chains are able to quickly confirm the wiring between small clusters of standard cells, but Trojans can evade detection by including an honest copy of the affected logic. IRIS confirms that a given cluster of logic being tested by a scan chain is approximately the right size. The search perimeter for rouge cells is reduced by running the scan chain test at high speeds. Ideally, the total bounds are tight enough to rule out the existence of sufficient extra logic to evade detection in scan chain testing.
In other words, what IRIS can’t directly image, the scan chain has to make up for with complexity of test. Thus, at 130nm, a simple bit-shift scan chain may be sufficient, since individual gates are resolvable; at 22nm, a more complicated technique splitting the scan chain into multiple segments, capable of challenging the system with mutually unpredictable data patterns, may be required to drive up the lower bound on circuit complexity to the “dozens of logic gates” range required to bypass the test. And at the most advanced nodes, even more scan chain segments may be required along with supplementary design techniques to drive the lower confidence bound into the “hundreds of logic gates” range for reliable Trojan detection with IRIS.
In general, when I use the term “IRIS” alone in a context where high-confidence gate level verification is required, readers should infer that I’m referring to some kind of hybrid verification technique of both IRIS and scan chain.
That being said, I envision IRIS mainly being used to verify high-value circuitry, such as those found in a discrete cryptographic enclave intended to store secrets such as root keys. These enclaves would not require the performance or density of the latest process nodes. With careful design, a 22nm or 28nm process can offer GHz clock speeds, sufficient for storing and processing bulk data with root secrets. The “2x” nm node is particularly interesting because it is the best “value per transistor” sweet-spot, and likely to stay that way for the foreseeable future: it’s the smallest process node that still uses the easier-to-fabricate planar CMOS transistors while requiring only single-patterning DUV lithography techniques.
Thus, the bulk of my on-going research will focus on samples produced in 130nm and 180nm (because there are Open PDKs available for those nodes today), and 22nm (because of the ultimate economic importance of the node). I am also betting that while the 2x nm node is not open source today, it will become more open within the next decade if the world continues on a “business as usual” scenario where technology continues to race down the commodification curve, and fabs continue to compete on price and need more designs to keep them busy and profitable.
While the imaging system has met its initial goals, the software still has miles to go before I sleep (And miles to go before I sleep). In particular, I’m still working on training a computer to automatically recognize patterns of gates in IRIS images and to generate a gate count census. I’d also ideally like to find a way to use formal methods to place an upper bound on the amount of logic one can hide in a scan chain for a given testing methodology, so designers can have a formally proven tool to validate that their scan chains are sufficiently dense so that IRIS can pick up any attempts to bypass them. Unfortunately, I’m neither a software engineer nor a mathematician, but the problems are interesting enough that I’ll still give them a go. Worst case, I will learn something new along the path to failure.
Above is the IRIS machine that I’ve built. There’s a lot going on here – but basically, it’s an IR camera attached to a microscope, a nanometer-resolution focusing mechanism, and a pair of 1050nm light sources that have continuously adjustable azimuth and zenith. This microscope assembly is mounted in a Jubilee motion platform. The Jubilee is open source, and was designed by Sonya Vasquez of Prof. Nadya Peek‘s Machine Agency group. I got it as a kit from Filastruder. The base motion platform is capable of 10 micron steps, and features a kinematically coupled Z-bed with three independent actuators, allowing me to dynamically compensate for planarity issues in the sample undergoing imaging.
Above is a short video loop showing the core mechanics in action. The weird thing on the bottom with the red and black wires coming out of it is the kinematically coupled nanometer-resolution fine focus stage; its motions are too small to be picked up by the camera.
An explicit goal of this project is to open source all of IRIS, so that anyone can replicate the imaging system. Democratizing chip verification is important because a credible threat of being caught reduces the incentive of adversaries to deploy expensive Trojan-implantation capabilities.
With little fear of being caught, there’s a payoff even if an adversary has to plow tens of millions of dollars into a capability for planting chip-level hardware Trojans in high-value targets. However, if chip inspection equipment can purchased in the ballpark of hundreds to perhaps thousands of dollars, and more than a handful of users are known to routinely inspect chips, the path to payoff for an adversary before they are caught becomes murky. In this case, a rational adversary may be deterred from targeting an IRIS-enabled design, instead reserving their capabilities only for the chips that are difficult to inspect.
Aside from that, I’ll be straight with you – a big motivation for IRIS is simply because I am curious, and I want to look inside chips and see how they are built (and it’s kind of fun and strangely satisfying to build robots). I haven’t been disappointed with what I’ve seen so far – I have to stop myself from wasting evenings browsing through the construction of chips. I’ve done a bit of chip design in the past, and it’s fascinating to see the diversity of techniques and new trends in chip designs. I’m excited to share this sense of wonder with kindred spirits!
Given the volume of material to cover, I’m going to break the documentation up into a series of blog posts that go into the methodology used to build the machine, as well as details about every custom component, and the design decisions that went into them. I’ll also summarize the status of the analysis software that accompanies the system – so stay tuned for more posts!
However, if you’re impatient and don’t want to wait for the documentation, you can already browse the source files for the microscope, control software, stitching software, and layout extraction software.

Finally, a big shout-out to NLnet and the European Commission. NLnet’s NGI0 Entrust fund, established with support from the European Commission’s Next Generation Internet Program, are instrumental in facilitating my work on IRIS. Also a big shout-out to my Github Sponsors for their incredible generosity and monthly support. Thanks to all these donors, I’m able to keep IRIS 100% open source and free of conflicts of interest with commercial investors.